This is part 2 of a four part series in the Energy Diagram Module. Stay tuned for the other parts!
To see part 1 click here.
In order to talk about energy of the reaction, a few key concepts are needed.
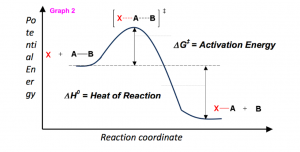
- If the products have less potential energy than the reactants, the reaction will release a net amount of energy (an exothermic reaction).
- If the products are higher in energy than the reactions, the reaction will consume a net amount of energy (an endothermic reaction).
But, in order to predict how well a reaction will progress, or how spontaneous the reaction will be, enthalpy is insufficient to make this estimation. Therefore, we rely on the thermodynamic calculation of Gibbs Free Energy (ΔG0) which is represented by the equation;
ΔG0 = ΔH0 – TΔS
The components of Gibbs Free Energy are:
- Enthalpy, ΔH0 – The heat consumed or released by the reaction.
- Temperature, T – Temperature of the system.
- Entropy, ΔS. The change in the degree of disorder.
The sign of the reaction indicates the release (negative) or absorption (positive) of heat during the reaction. Therefore, if ΔG0 is negative the reaction is always spontaneous. Similarly, if ΔG0 is positive the reaction is never spontaneous. When ΔG0 equals zero, the reaction is at equilibrium. In accounting for these additional thermodynamic properties using Gibbs Free Energy, different terms are used.
- If a reaction has a negative ΔG0 , it is therefore spontaneous and is said to be exergonic.
- Conversely, a reaction that has a positive ΔG0 is not spontaneous is considered endergonic.
Graph 2
(click on photo to enlarge)
With the addition of the temperature variable in the Gibbs Free Energy equation, it is easy to see that an endergonic reactions can be driven forward simply by increasing the temperature of the reaction so that the term TΔS is more negative than ΔH0, thus making ΔG0 negative and making the reaction spontaneous!